一.什么是强化学习
1.1 强化学习的要素
主体:主体可以是一个抽象的概念,它通常被理解为“动作的执行者”或“游戏的主角”。
环境:环境是无法被主体直接操控的,但可以被主体的动作改变,例如超级码力中可以才踩蘑菇,alphago的围棋落子,占据棋盘。
动作: 主体对环境实施的影响,在我们的游戏中,就是选择向上飞或者向下飞。
奖励: 执行动作后,环境对主体的反馈。例如撞到柱子-1分,通过柱子+1分。
策略:用什么样的方式来让reward尽量达到最大。比如我们选用的Epsilon策略。
1.2 强化学习的特点
- 做中学。我们无法将主体的行为明显地区分为学和做两部分,这和传统的机器学习方法不一样。传统的机器学习方法都是分成训练过程和测试过程。而强化学习不同,它必须一边学一边行动。
- 综合考虑与平衡短期回报和长期回报。这是因为我们的系统不一定存在及时的反馈。很多时候,主体做出一个动作并不知道好不好,只有当一系列动作执行完毕之后,主体才发现原来自己踩到了一颗地雷,从而学习到这一些列过程都是错误的。当然也存在一些相反的情况,例如虽然主体可能通过一系列动作暂时得到不错的回报,但是从更长期的角度来看,主体收到的punish远大于reward。这就是所谓的短期回报和长期回报的平衡,在下棋游戏中,这种平衡的重要性被体现的淋漓尽致。
正是因为有了这两个特点或者难点,强化学习比一般的机器学习算法要困难得多。


通过观察-行动-再观察-再行动的方式来获得最大化奖励

二.Q-learning算法
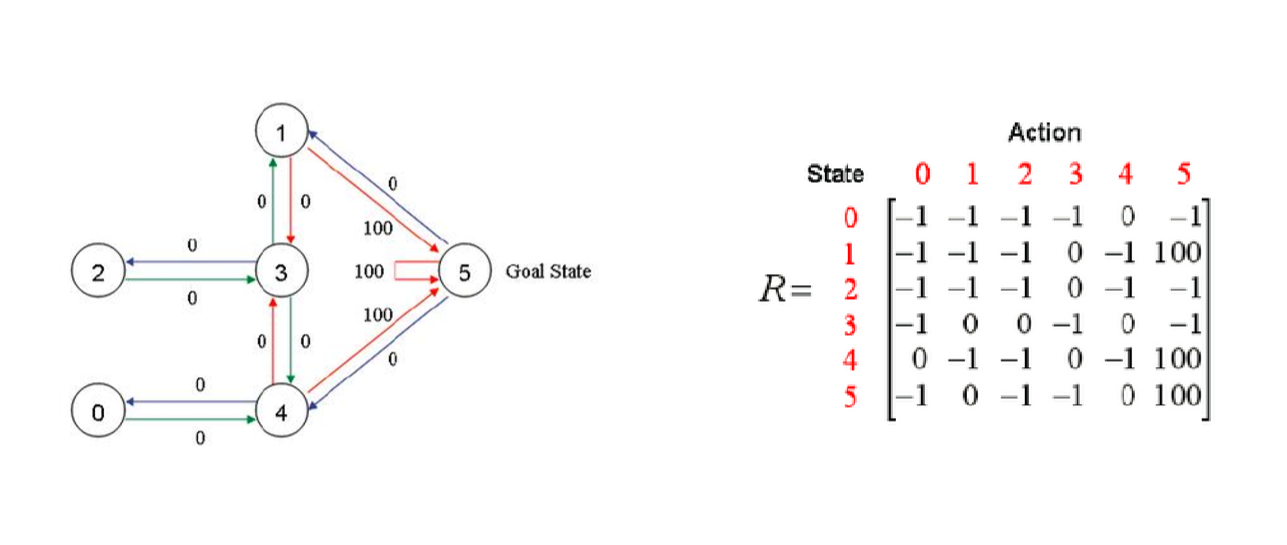
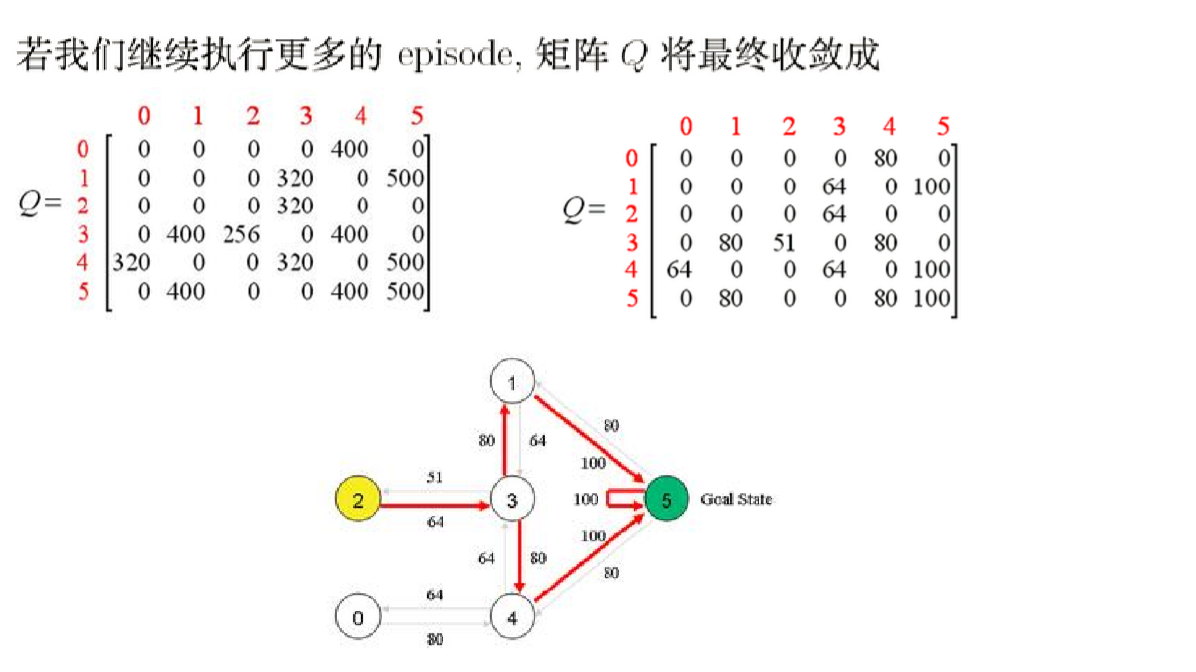
1.假定我们拥有这样的一个房间,用有向联通图来描绘表示它的可达状态
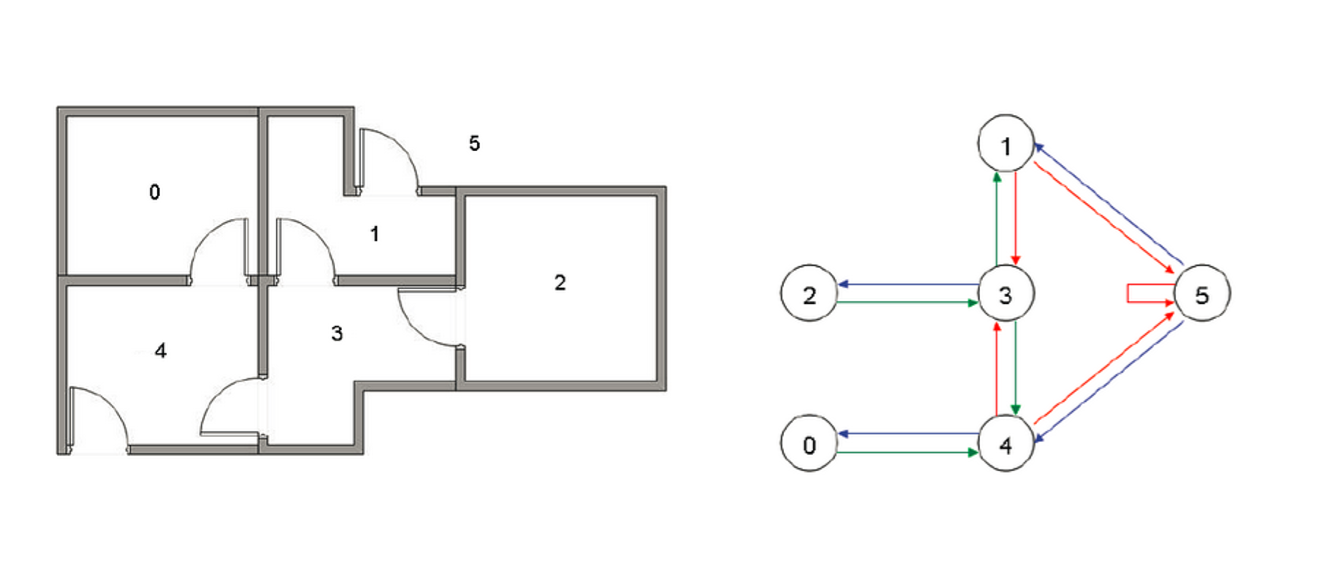
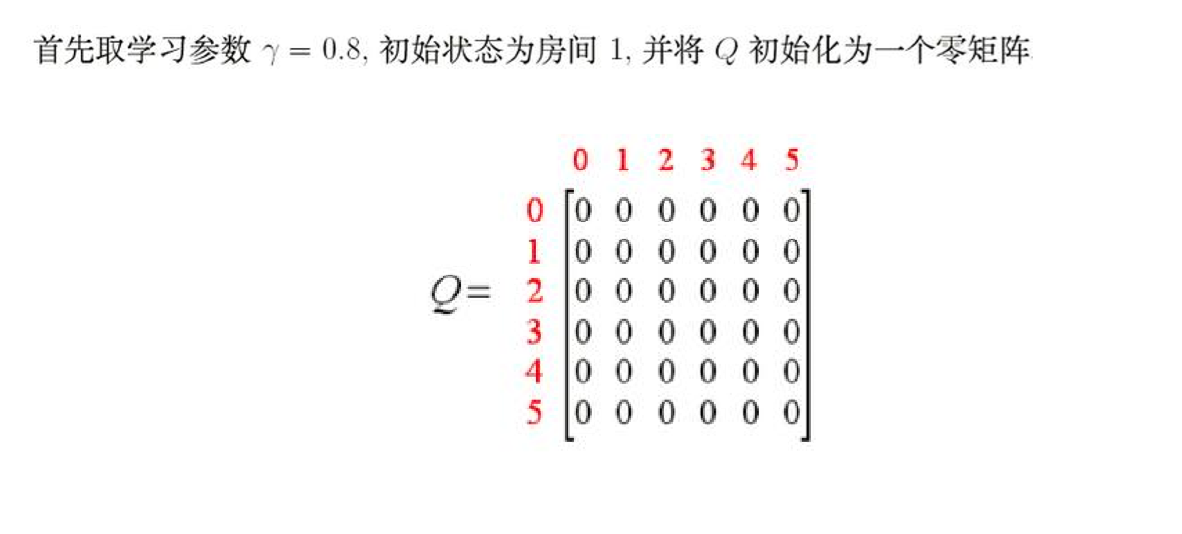
2.用邻接矩阵R来描绘出表示连通图(-1不可达,0表示可达但reward为0,100表示可达reward 为100),并初始化Q矩阵

算法描述
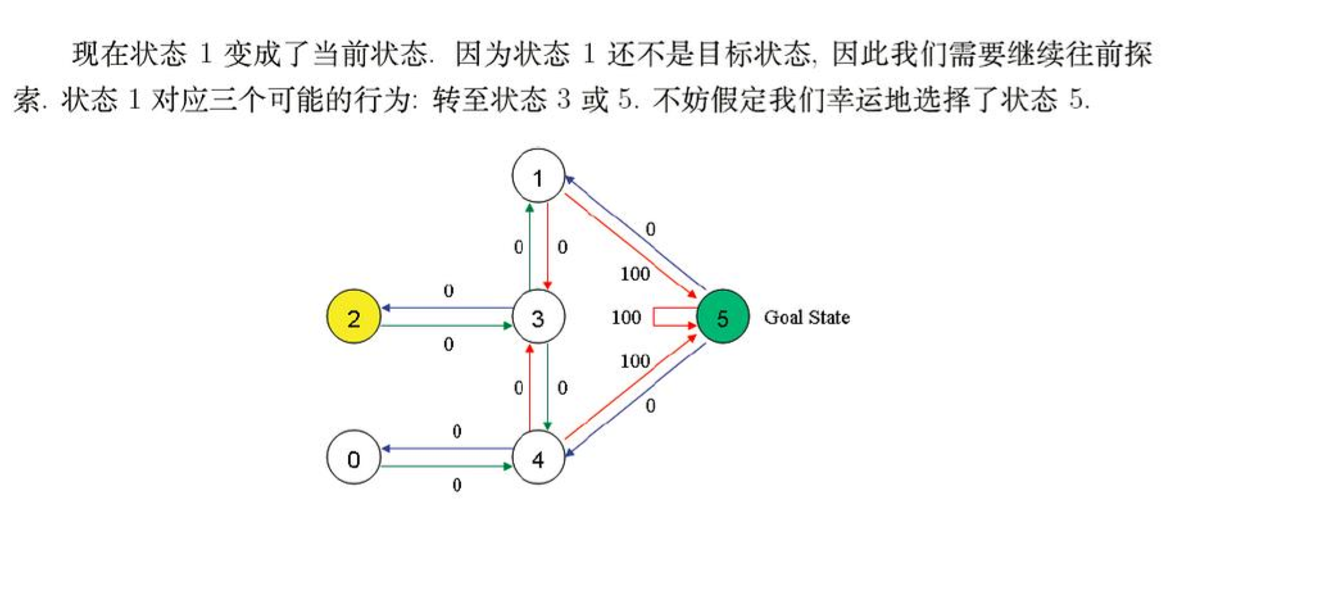
3.模拟行动

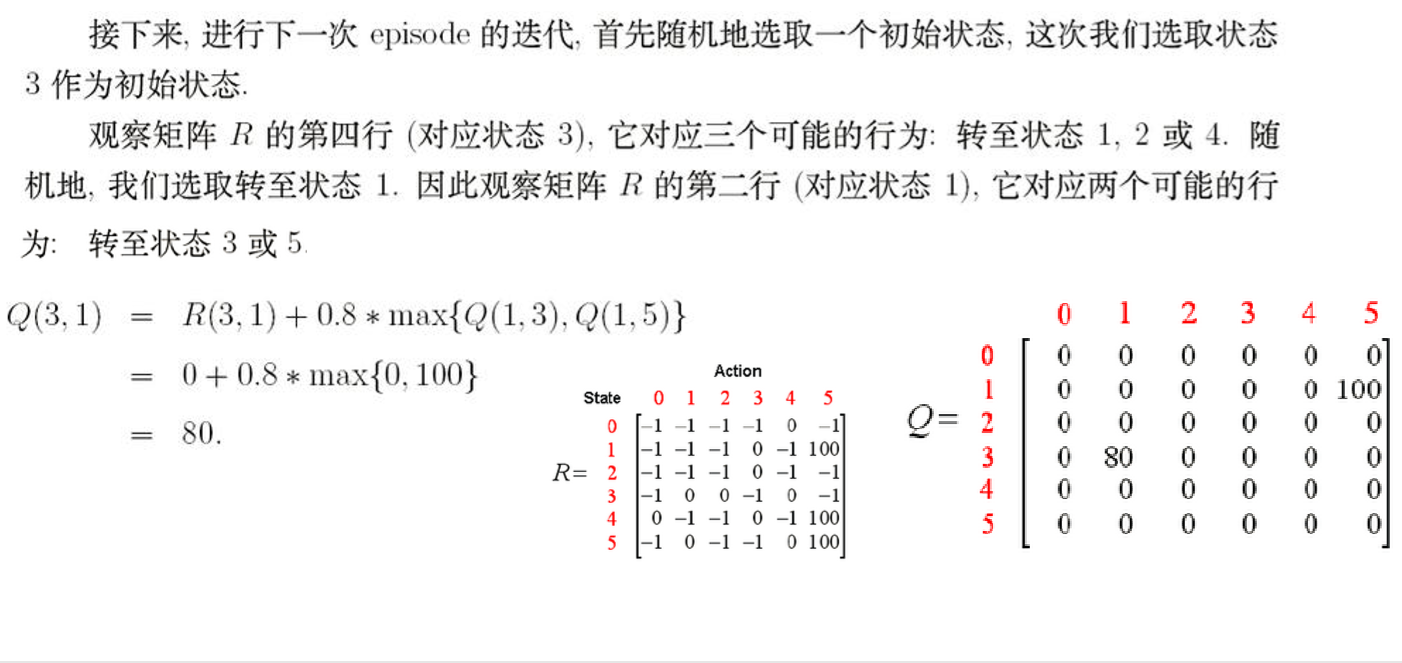
4.最终的Q表
二.Flappy Bird中的DQN架构
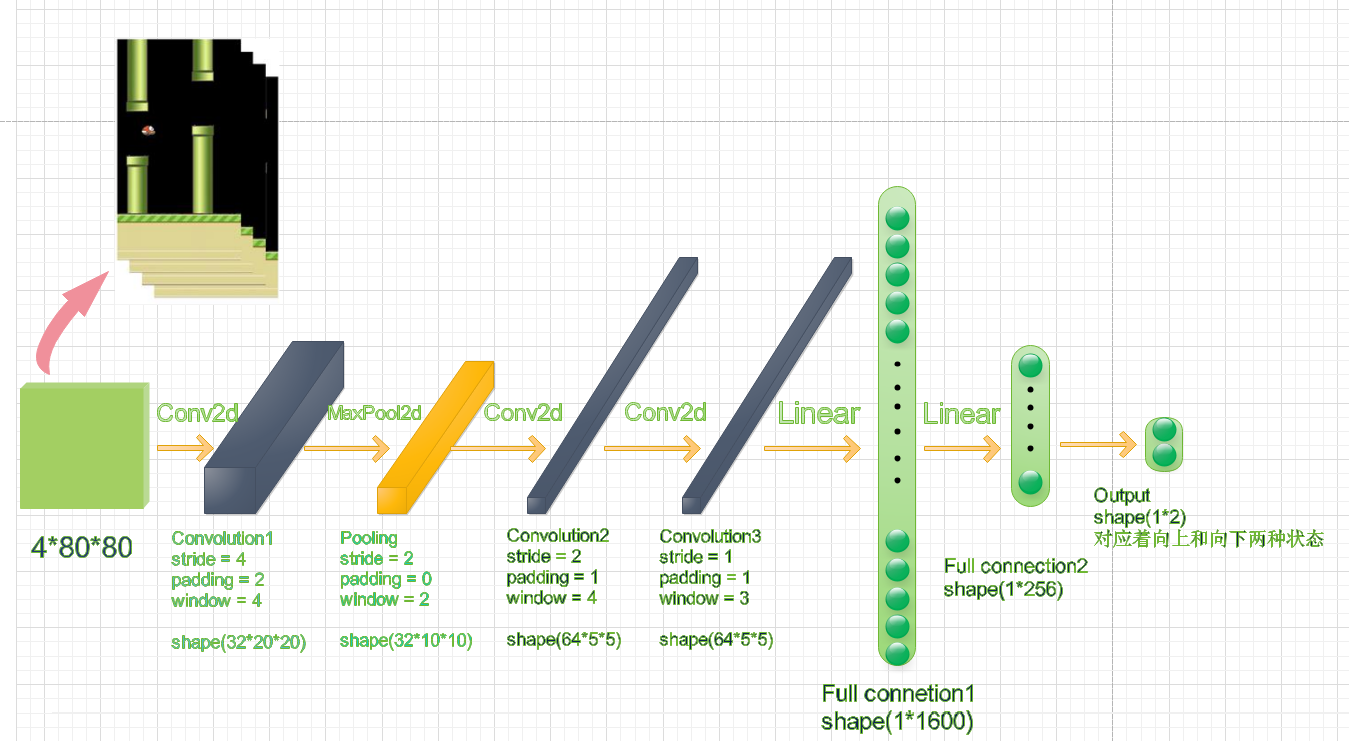
首先我们要明确系统架构,该神经网络的输入时基于PyGame实现的Flappy Bird的画面,输出是游戏中,小鸟的动作所对应的Q函数。具体来讲,因为小鸟的动作只有向上和向下两种。所以,output的值就是向上和向下对应的Q值。
我们采用的是当前t时刻的连续四帧画面作为网络的输入。整个网络采取了一个卷积神经网络的架构,它的输入是一个四通道,80*80大小的图像,不同的通道对应了不同帧的时间步骤画面。
三.程序的运行
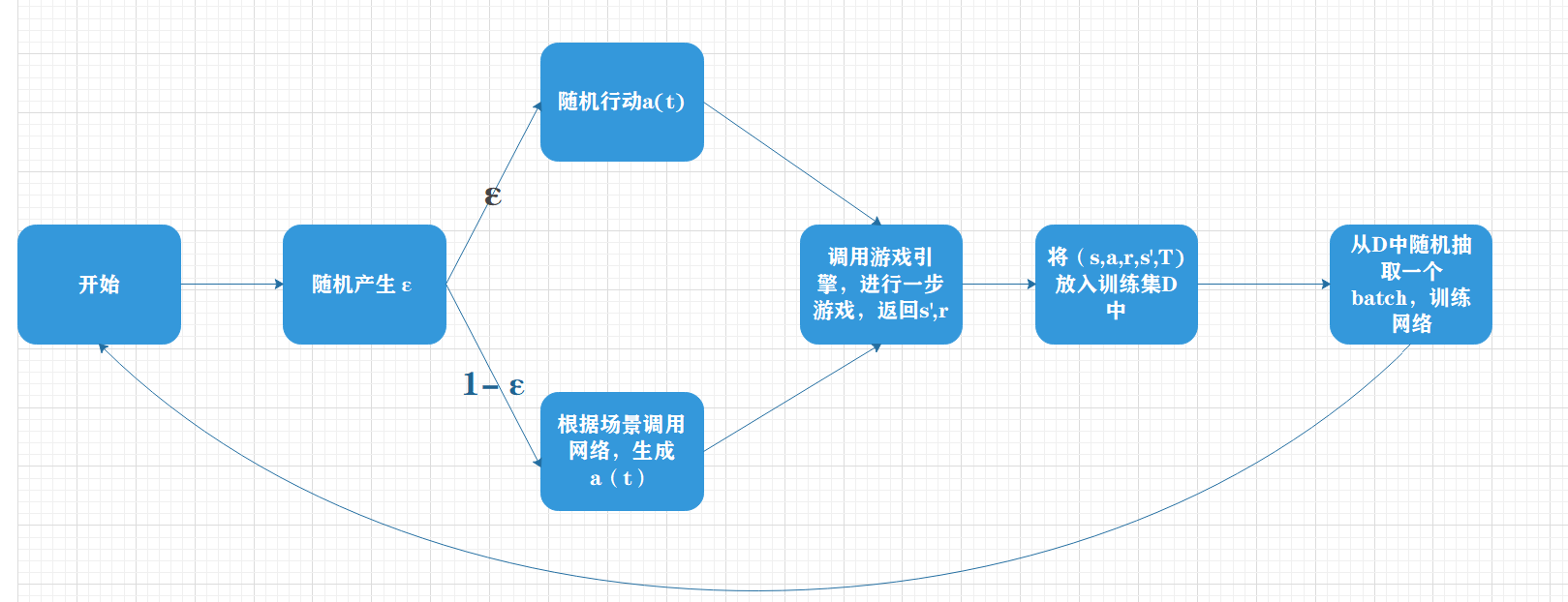
首先,每个周期主体都会将最近四个周期的游戏画面s输入到DQN神经网络中,并输出两个Q值,分别对应主体选择向上运动和向下运动的估值。之后,主体会在这两个Q值中选择最大的一个,并采取响应的行动。
由于开始模型的能力很差,所以主体会以每个周期Epsilon的概率随机选择一个动作,而更多的时候则按照神经网络的结果行动。这里的Epsilon是一个概率值,它会从早期的INITIAL_EPSILON一点点地减少到FINAL_EPSILON,减少的速率基本上是超参数EXPLORE的倒数,也就是说,主体在早期会经历一段野蛮的探索期,较多地选取随机行动。探索期结束后,他才会最大概率地按照神经网络的指挥行动。这种方案被成为Epsilon贪婪策略。
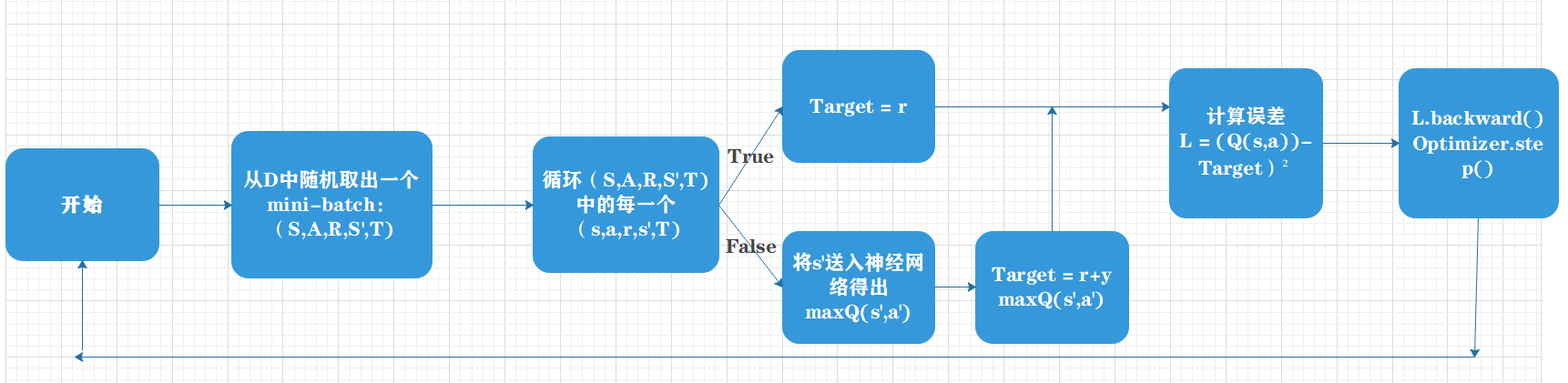
接下来,主体会将前四帧画面s,后四帧画面s’,这一次采取的行动a,游戏给的回报r和游戏是否结束t记录下来形成一个五元组D(s,a,r,s’,T),D的数据类型为deque(双端队列)。其中,T是布尔值。D具有存储容量的限制,由超参数REPLAY_MEMORY限定,当D中存储的五元组的数据超过这个值的时候,会进行POP_LEFT操作,即删除组老的一个五元组。
当游戏进行到obeserve个周期之前,神经网络的训练是不会展开的,主体只会利用神经网络来做决策行动。而到了oberserve个周期之后,训练才会与主体的决策同步进行。在训练的时候,主体会从D中随机抽取出BATCH个五元组作为当前的一匹数据(即mini-batch)来训练神经网络。
具体到每一次的训练,主体会将这批数据拿来,先将他们的s状态和行动a输入网络,得到评估值Q;之后再将s‘状态输入网络,得到下一时刻两个动作中最大的估值Q’,从而计算出目标函数之 r + GAMMA*Q’;于是,我们可以将Q和r + GAMMAQ’ 做差值,平方得到损失函数。然后,运行反向传播算法,更新网络的权重。